Identifying Polyhedra Enabling Memorable Strategic Mapping
TRANSCEND MEMBERS, 22 Jun 2020
Anthony Judge | Laetus in Praesens - TRANSCEND Media Service
Visualization of Organization and Strategic Coherence through 3D Modelling
Introduction
22 Jun 2020 – Strategies, declarations and sets of values and principles typically take the form of lists with a specific number of items. The number selected often varies between 8 and 30. Examples are the 8 Millennium Development Goals of the UN and the 30-fold Universal Declaration of Human Rights. Currently a major focus is given to the 17 Sustainable Development Goals of the UN. There is seemingly a total lack of explanation as to why any given number is appropriate. Nor is there any interest in how such patterns may be more or less appropriate from a systemic perspective. Little consideration is given to the manner in which the items noted in each case are related — let alone how the many different strategic articulations, based on different choices of numbers, are related to one another.
It is possible to imagine that each such set could be mapped onto a polygon in 2D with a distinctive number of sides — potentially reflective of seats around a negotiation table. It is also possible to explore how the elements of any such articulation could be mapped in 3D onto a polyhedron — to be variously rotated for inspection in virtual reality. Possibilities in that respect are discussed separately (Psychosocial Implication in Polyhedral Animations in 3D, 2015; Towards Polyhedral Global Governance: complexifying oversimplistic strategic metaphors, 2008).
Especially relevant to this argument is how any such mapping increases memorability and communicability — and how it enables the set to be comprehended as a whole. These considerations can be considered vital to any sense of coherence of the set as an integrative pattern — as distinct from a simple checklist or a “to do” list. Are many people able to recall the elements in the patterns identified in the following, or why they include the number of elements in each case:
- 10-foldness: Habitual use of a 10-fold strategic framework?
- 12-foldness: Checklist of 12-fold Principles, Plans, Symbols and Concepts: web resources
- 20-foldness: Checklist of web resources on 20 strategies, rules, methods and insights
The question in what follows is what makes for memorability in the face of a relatively complex set of principles or elements in a strategy. This question assumes that global governance is faced with a fundamental cognitive challenge, as argued separately (Comprehension of Numbers Challenging Global Civilization, 2014). Is the set of 17 Sustainable Development Goals as “comprehensible” or “memorable” as might be assumed to be necessary for their coherent global governance? The challenge of comprehending the risk of civilizational collapse may be in some way related to any tendency to represent it by use of a 2D “mind map” (Mind Map of Global Civilizational Collapse: why nothing is happening in response to global challenges, 2011).
Framed otherwise, the question is at what number does coherence and memorability start to erode in the case of a 2D pattern of “constructible polygons“. When does the number of representatives around a table characterize fragmentation rather than coherence? Configured in 3D, the question can be framed in terms of the number of “constructible polyhedra”, a pattern which is not seemingly explored to the same degree as in the case of polygons. In quest of greater systemic coherence, the exercise which follows is an exploration of the polyhedra which might be suitable for mapping a strategic articulation, depending on the choice of numbers of elements.
In a period in which collective memory is variously challenged, it should be emphasized that the following exercise is primarily concerned with memorability (Societal Learning and the Erosion of Collective Memory, 1980). There is a very extensive mathematical literature on polyhedra from a variety of perspectives. The literature does not seem to engender or order polyhedra in terms of their suitability for mapping.
Although memorability and mapping are not the focus in such studies, extensive use is made of polyhedral frameworks in computer compiler techniques for analysis and transformation of codes with nested loops (also termed the polytope model). This is indicative of the relevance of the approach to the analysis of patterns of feedback loops which characterize the relation between the many strategic problems (Feedback Loop Analysis in the Encyclopedia Project, 2000). A more general review of information mapping is offered by L. John Old (Information Cartography: using GIS for visualizing non-spatial data Proceedings, ESRI International Users’ Conference, 2002).
Mathematics has indeed developed far more sophisticated tools to explore polygons, polyhedra and polytopes in N-dimensions. As the realm of specialists, these are typically unrelated to any criteria of memorability, comprehensibility or communicability. The quest for comprehension of the symmetry associated could be understood as implying such a preoccupation (Dynamics of Symmetry Group Theorizing: comprehension of psycho-social implication, 2008).
As the epitome of preoccupation with patterns of order and relationships, there is some irony to the fact that, in organizing itself — as in the Mathematics Subject Classification — mathematics is curiously challenged by reliance on the simplest methods of order, namely the nested hierarchy (Is the House of Mathematics in Order? Are there vital insights from its design, 2000; Towards a Periodic Table of Ways of Knowing — in the light of metaphors of mathematics, 2009).
The associated thinking could be said to reinforce the nested structures typical of strategic articulations. Thus the UN’s 17 Sustainable Development Goals clusters 169 targets, with little consideration of how these are interrelated, even though the 17th Goal (“Partnerships for the Goals”) is concerned to a degree with their coordination, namely to: Strengthen the means of implementation and revitalize the global partnership for sustainable development. Is a 17-fold pattern inherently “forgettable”?
From the perspective of memorability, such challenges could be explored in terms of the skills of a mnemonist, most notably the method of loci, as described by Frances Yates (The Art of Memory, 1966). This is a strategy of memory enhancement which uses visualizations of familiar spatial environments in order to enhance the recall of information. It is associated with the term topoi (from the Greek for “place”) as a metaphor introduced by Aristotle (Topics). These characterize the “places” in memory where a speaker or writer may “locate” arguments that are appropriate to a given subject — as mnemonic aids (Richard Nordquist, Definition and Examples of the Topoi in Rhetoric. ThoughtCo, 12 February 2020).
Understood otherwise, this is the modern derivation of topics. A topic map in two-dimensions is upheld as a standard for the representation and interchange of knowledge, with an emphasis on the findability of information. The Topic Map paradigm has been adapted to the web by an international consortium (Benedicte Le Grand, Topic Map Visualization, January 2003). The possibility of its adaptation to 3D and virtual reality has been envisaged (Alexandre Rocha Oliveira et al, Supporting Information Visualization through Topic Maps, Educational Technology, 2002)
The question here is how the vertexes, edges and faces of polyhedra can be used as “topoi” or “loci” such as to provide a higher order of coherence to the strategic pattern which connects the information associated with them. The role of music in rendering such patterns memorable is discussed. The argument concludes by highlighting the developing insights of logic into the geometry of opposition and the manner in which alternative patterns of connectivity are reframed by particular polyhedra.
This is seen as a specific response to the currently problematic degree of divisiveness, fragmentation and disagreement in governance at all levels of society. In extraordinary times, there is a case for recognizing that extraordinary polyhedral forms may offer insights into unforeseen approaches to governance and requisite connectivity. The many examples presented then raise the question as to how global governance might be imagined in that light — if only by the future.
*********************************************************************************************
Memorable mapping possibilities: The challenge of rendering a pattern of 16(+1) strategic goals coherent, memorable and communicable can be variously explored:
- Using a Rubik cube: Interplay of Sustainable Development Goals through Rubik Cube Variations: engaging otherwise with what people find meaningful (2017)
- Using a star torus: An earlier exploration focused on the pattern of 16 articulated by the star torus, since the 17th is specifically intended as coordinating the others, then to be understood as somehow centrally located as a point of focus (Current relevance of the “simplest torus”? 2019; Modifying the cyclic symmetry of the star torus, 2019).
As a mnemonic mapping aid, the star torus enables a variety of relevant considerations of a 16-fold pattern, as indicated by other sections of that argument (Framing an operating context of 16 “dimensions”, Functional dynamics of a 16-fold configuration of strategic goals). Of particular interest, is the manner in which the cyclicity of such a torus can be varied to interrelate otherwise disparate mapping configurations — including the 8-fold and the 12-fold.
| Illustrative use of geometry of star torus for mapping purposes (use browser facilities to enlarge animations and labelling) |
|||
| 5-fold | 8-fold | 12-fold | 16-fold |
 |
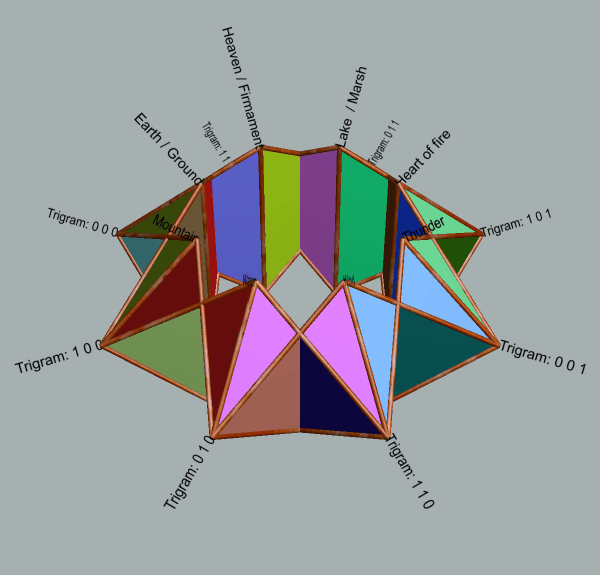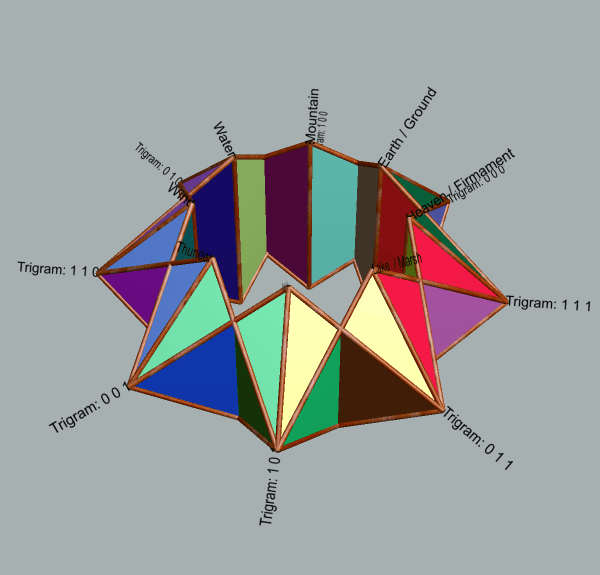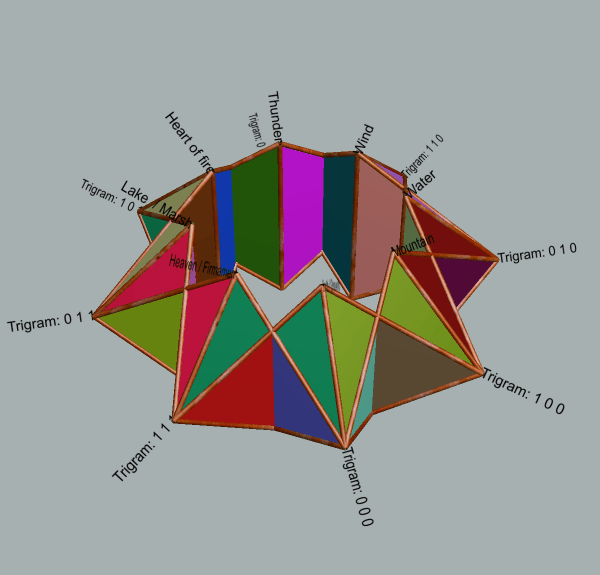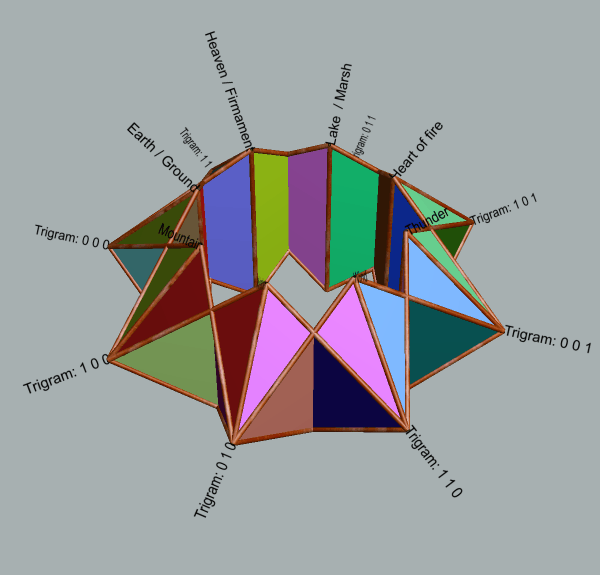 |
 |
 |
| Reproduced from discussion in Global Coherence by Interrelating Disparate Strategic Patterns Dynamically Topological interweaving of 4-fold, 8-fold, 12-fold, 16-fold and 20-fold in 3D (2019) Animations generated with Stella Polyhedron Navigat |
|||
Rather than focusing on 16 as a means circumventing the difficulty of mapping 17, an alternative approach that can be explored is through mapping 34, namely 2×17. In such cases, 17 can then be associated with the axes linking 34 vertexes, or the parallelism of 34 edges or 34 sides. Examples of unusual possibilities — and therefore potentially memorable — are indicated below.
| Contrasting possibilities of mapping 17 SDGs onto polyhedra (as 2×34 features) | |||
| Moon base | Dual of 4-frequency tetrahedral geodesic sphere | Stewart Z4 | Gyroelongated square bicupola |
| 34 vertexes (12 types), 63 edges (21 types), 31 faces (11 types) | 34 faces (4 types), 96 edges (8 types), (64 faces (6 types) | 22 faces (11 types), 34 edges (17 types), 14 vertexes (8 types) | 34 faces (5 types), 56 edges (8 types), 24 vertexes (3 types) |
 |
 |
 |
 |
| Animations generated with Stella Polyhedron Navigat | |||
Mapping the unimaginable: The associated challenge of providing a degree of coherence to the “unmappable” pattern of 169 could be explored by a similar process, namely a focus on 378 (2×169), as indicated in the reasonably memorable pattern on the left below.
| Indicative mappings | ||
| 169 SDG tasks onto 378 features | Configuration of Szilassi polyhedra | |
| Squares+Heptagons | 6 | 7 |
 |
 |
 |
| 378 faces (15 types), 798 edges (29 types) 420 faces (15 types) | Interactive 3D; variants (vrml; x3d); videos (solid mp4; wireframe mp4). | Interactive vrml; Video mp4 |
In this light, it might be usefully asked how 7-fold articulations can be usefully mapped, given the significance attached to that number as being an appropriate (“comfortable”) size for a meeting, or a strategic articulation, especially in the light of the classic study by George Miller (The Magical Number Seven, Plus or Minus Two: some limits on our capacity for processing information, Psychological Review, 63, 1956, 2).
One notable candidate in that case is the highly unusual Szilassi polyhedron of 7 sides — all touching one another. This possibility is discussed separately (Mapping of WH-questions with question-pairs onto the Szilassi polyhedron, 2014; Dynamics of discord anticipating the dynamics of concord, 2018).
TO CONTINUE READING Go to Original – laetusinpraesens.org
DISCLAIMER: The statements, views and opinions expressed in pieces republished here are solely those of the authors and do not necessarily represent those of TMS. In accordance with title 17 U.S.C. section 107, this material is distributed without profit to those who have expressed a prior interest in receiving the included information for research and educational purposes. TMS has no affiliation whatsoever with the originator of this article nor is TMS endorsed or sponsored by the originator. “GO TO ORIGINAL” links are provided as a convenience to our readers and allow for verification of authenticity. However, as originating pages are often updated by their originating host sites, the versions posted may not match the versions our readers view when clicking the “GO TO ORIGINAL” links. This site contains copyrighted material the use of which has not always been specifically authorized by the copyright owner. We are making such material available in our efforts to advance understanding of environmental, political, human rights, economic, democracy, scientific, and social justice issues, etc. We believe this constitutes a ‘fair use’ of any such copyrighted material as provided for in section 107 of the US Copyright Law. In accordance with Title 17 U.S.C. Section 107, the material on this site is distributed without profit to those who have expressed a prior interest in receiving the included information for research and educational purposes. For more information go to: http://www.law.cornell.edu/uscode/17/107.shtml. If you wish to use copyrighted material from this site for purposes of your own that go beyond ‘fair use’, you must obtain permission from the copyright owner.