Structural Analysis and Chemical Models
FEATURED RESEARCH PAPER, 23 Apr 2018
Johan Galtung - TRANSCEND Media Service
1. Introduction
1974 – We assume “structural analysis”, like “functional analysis” and “causal analysis”, to be a thought form, a way of casting social analysis. It is not a theory, and certainly not a proposition. Nor is it a paradigm, for that is something more specific, where a choice of units and variables has already been made. On the other hand, there may be paradigms within, or based on, the basic perspective of structural analysis.
Structural analysis differs from functional analysis not by rejecting any interdependence axiom, but by not assuming any kind of goal-directedness. There is no dichotomy between a structural and a functional side. Structuralism, we assume, refers to something “purely structural”; structure, then, understood in the traditional mathematical sense: s : (E, R) where E is a set of elements e1, e2, …, en, …. and R is a set of relations (including operations) defined on E.
This is a very general definition. The task of the structuralist is to identify E and R in such a way that it leads to fruitful social analysis, and “makes” out of social systems more than a set of detached actors — a “whole”, something connected that can be treated as an entity, however internally complex it may be1.
So far this would not necessarily differ from the structural side of what functionalism deals with. A functionalist, whether of the conservative, liberal or radical variety, would definitely have to include in his analysis a set of structural elements. In careless functional analysis there is a tendency to regard these elements as mutually unrelated, only to be seen in the light of their functions, not in the perspective of how they relate to each other. In more careful functional analysis, however, interstructural analysis would be an integral part of the total scheme2.
Structuralism, as a special type of structural analysis, obviously has to add something to the idea of structure as an interrelated set of elements, just as classical functionalism adds a variety of assumptions. Three ideas can be singled out for attention, without claiming in any way that they exhaust the assumptions made, nor that anything referring to itself as structuralism necessarily has to make all of these assumptions.
First, there is an idea which is actually contained in the definition of structure, but should be spelt out. Structuralism makes for a richer content on the structural side, among other methods by means of meta-relations, by introducing relations between relations. Example: the relation between a wife and her brother has to be the opposite of the relation between the wife and her husband (if the former is close and warm, then the latter is remote and cold, and vice versa). In this case two bilateral relations are defined in a set of kinship elements, one positive (close, warm), the other negative (remote, cold), and then it is postulated that for some specific pairs the relations cannot be the same. But this is only another way of saying that three elements (husband, wife and brother) are related in a certain way, in other words that a trilateral relation is defined in addition to the two bilateral ones3.
In less mathematical terms what this says is simply that not only are elements interdependent, but so are relations. If you change one (e.g. the wife and her brother come closer to each other), then the other will also change (wife and husband become more removed from each other). In a sense this is nothing more than what is already contained in the functionalist assumption about interdependence in a structure (for it was never assumed that this applied to B only, and not to R); but it is spelt out, and in a very important way. In general, the denser the web of interrelations, the more holistic the image given, the more removed from the actor level.
This way of thinking is basic to Lévi-Strauss’s analysis of myths and kinship relations. If a, b, c, d,. . . x, y, z, w, are mutually opposed elements (which in also quadrilateral) this can be used to “find” a fourth element, in myths (right-left, cru-cuit, etc.) then Lévi-Strauss’s analysis has at its basis a quadrilateral relation that may be seen as a meta-relation between two bilateral relations:
a : b :: c : d or x : y :: z : w
which reads “a relates to b the same way as 0 relates to d”, or “x relates to y the same way as 2 relates to w”. As in a proportionality relation (which is also quadrilateral), this can be used to “find” a fourth element, or for a systematic comparison of elements in two different systems — two different myths, one myth and one culinary system, etc. It can also be used across two (or more) quadrilateral relations, as indicated above: if the relation between a and b changes to that between x and y, then a cor- responding change has to be brought about for the relation between c and d. To blame Levi-Strauss for not always having brought this on a precise form so that others can come to the same results as he does is not quite unwarranted4,“‘but important here is the perspective, not the precise method, at least to start with. In his cooperation with leading mathematicians of the Bourbaki school, such as André Weil, he has added the idea of mathematical calculus to the many formulations in verbal prose — particularly the calculus of permutations5 — and with great succe.
Second, there is the very seminal idea of the deep structure, as opposed to surface structures. There is more to this than just the idea of an “essence” to which some “accidental” elements have been added — elements that the analyst has to abstract away from in order to come to grips with the deeper elements. It is perhaps not too different from Lazarsfeld’s latent structure, which is also regarded as something more constant, and perhaps “cleaner”, “simpler” than empirical reality. Once alerted to it, however, we can probably “see” the deep structure — making it more “empirical”.
Most important here is Chomsky’s approach, which is an implicit and explicit rejection of the idea that the mind is a tabula rasa open to any cultural imprint through learning, which in turn is based on reinforcement mechanisms. This behaviorist assumption is rejected on at least three grounds: children are able to create many more correct sentences than they have ever “learnt”, people learn even difficult natural languages more easily than artificial languages; and although languages are complex, they can be seen as essentially simple variations over a limited variety of elements. For these and other reasons the conclusion is drawn that man is born with a program that sets constraints on natural languages, but also provides built-in learning: when a child has some language elements they are fed into his program, which then turns out correct sentences6.
This sounds reasonable. But it raises such questions as whether the “program”, possibly even present in the genetic code, is similar in all human beings, and whether it is unchangeable, ontogenetically and/or phylogenetically. One possible answer would be in terms of a deep structure with an irreducible common nucleus surrounded by changeable elements. But this answer also brings into structuralist reasoning something immutable. This is very different from the implicit assumption so far, which has more or less been that Man is the intersection between Nature and Culture, and that whatever is Nature is rigid (immutable or governed by immutable laws), whereas whatever is Culture is flexible. Moreover, it only begs the question: where is the borderline between Nature and Culture? And where is Society? Marxists and positivists alike have assumed Society to be more on the Nature side, governed by objective laws, with the Marxist laws providing for transcendence into a qualitatively new reality, the positivist laws not. But with Chomsky and Levi-Strauss are we to understand that language and myths now are on their way from the Culture side to the Nature side?
This question actually leads to the third point which also relates to how structuralist analysis may differ from causal analysis: the fundamental idea of transformation. One kinship system, one myth, one grammar may be seen as a transformation of another, which is obvious if they are to be seen in terms of a common deep structure. However, transformation is not the same as causation. There is no implicit assumption that S2 historically came about through a process that may be interpreted as a transformation of S1 — all that is said is that a transformation may be defined that transforms S1 into S2. Obviously, invariant under this type of analysis is the deep structure.
If, now, these three aspects of structuralism are combined it is more easily seen why Lévi-Strauss’s analysis tends to be non-diachronic, atem- poral (which is not the same as saying that it is synchronic; rather, it is timeless). The analysis yields a system of rules (like in chess) rather than understanding of processes. Basic is the idea that there is a limited number of correct transformations or permutations of basic elements, limited by the common deep structure. Part of the deep structure, incidentally, is defined in terms of relations between relations. Understanding in this kind of thinking is not in temporal terms, neither causal (how did it come into being?) nor functional (what does it lead to?), but in transformational terms: how can this be seen as a transformation of other structures? That this is a form of understanding is obvious. It is also obvious that it represents a negation of the manipulative implications behaviorism so often has led to. But at the same time it is not clear that it leads to a more liberating perspective. All man can do seems to be to run through these permutations. In addition, it may also support thought forms where the area of the immutable grows and of the changeable diminishes, reducing Man’s Spielraum by making him more firm, but also more rigid7.
Leaving this problem aside, let us immediately emphasize that “structural analysis” is a wider category than “structuralist analysis”. Its point of departure is only the definition of structure given above, in which the idea of interdependence between relations would be included. There may be scope for a distinction between essential and accidental elements, but this is probably common to all science. Science is an effort to abstract away from some of the complexities of Nature, Society and Culture to get at “basic” relations, but these are not necessarily located anywhere, like a deep structure in the genetic code, more like the realist in rclms assumption. If pure deep structure could be located independently of the appearances of that structure (e.g. as a social structure crystalliring in times of crisis then it would of course be quite a different matter. It is useful, but not indispensable, if Weberian ideal types and Durkheimian elementary forms can be encountered empirically.
Without necessarily” being at issue ‘with structuralist approaches, let us rather formulate positively what we might like to ask of a structural analysis. What would be our list of requirements, so to speak?
Firstly, we do not think it should be construed in a way antithetical to radical, functional analysis. Rather, it should lead to far deeper understanding of the structural side. But there should still be room for values, and for goal-directedness in general, not only for the acting out or implementation of latent structures.
Secondly, we do not think it should be seen as antithetical to causal analysis either. The idea of cause and effect, which we understand simply to mean that a change in some variables is accompanied by a change in others, is not unreasonable. If it is thrown out because it may lead to manipulation and continued dominance in the hands of the Herr, then it is difficult to see that it is not also thrown out as a tool of liberation in the hands of the Knecht. But causation should not be interpreted too strictly: there should be room for the ideas of dialectic rather than mechanistic relations, of probabilistic rather than deterministic relations, of non-monotone rather than monotone relations and of conditional rather than absolute relations. Moreover, it should not be seen as a Law of Nature, as an invariance, but as a provisional invariance, that may be broken up if it no longer serves. But the idea that “changes somewhere can be brought about by changes elsewhere” remains. This idea can be used instrumentally and for prediction, and since both usages are found a perspective should embrace them (which is not the same as accepting them).
Thirdly, the idea of transformations should be a basic pillar of the system, but it should be linked to notions of functional and causal analysis so as to permit analysis in terms of transformations for what?, transformations to be brought about how? — in order to enrich these notions, possibly even embracing them.
Fourthly, the analytical system should be rich in terms of relations. More particularly, it should take into account that social structures are such that:
- relations vary in strength and may also be negative
- relations are asymmetric, not only symmetric
- relations are multilateral, not only bilateral
- relations are between elements at different levels of complexity:
- between statuses or actors in a system
- between the systems in a structure
- between the structures in a society, etc.
With these requirements in mind, let us look at two approaches to structural analysis of social systems: an old one (graph analysis) and a new one (utilizing chemical structures).
2. Structure according to graph theory
One of the most promising approaches, particularly heralded some years ago, was the idea of using graph theory as a basic tool in understanding social structure. Since structure is defined in mathematics as a set of elements connected by a set of relations, it looked as if one had a tool that was sufficiently close to some basic ways of perceiving and reasoning about social systems8. The elements could be identified with social actors (human beings, groups, nations, regions, globes), and the relations could be identified with relations of interaction (interaction as such, communication, dominance, power relations, exploitation relations and what not). Thus, one was led directly to what in social science is known as a social system: a set of actors interconnected by a set of interaction relations. Since “interaction” is a very general term, this formulation encompasses an enormous variety of social systems. Interaction means exchange of value but the value may be negative (as in a war) or positive. (as in a co-production relation) or it may be negative one way and positive the other (as in a slave owner-slave relation). The exchange’may be symmetric, on equal terms, or on unequal terms. The relation may be strong or weak, whether this is interpreted in terms of frequencies or in terms of the strength of the relation.
All this means that the stage is set for the utilization of graphs that not only connect the elements, but also measure the interactive relations, for instance on a scale from -1 (maximally negative value) to +1 (maximum positive value). It should be noted that the idea of asymmetric interaction means that one needs two arrows between two actors: one to indicate the value that flows in one direction and the other to indicate the counter-value. Unfortunately, this possibility also points to a weakness in the whole approach: what is possible and meaningful in mathematical graph theory is not necessarily translatable for the analysis of social systems, for even if measurement were possible measures might not be meaningfully combinable according to the simple operations and rules of conventional arithmetics.
However, as a figure of thought this system is nevertheless quite meaningful. One may now proceed in two important directions, both of them highly significant within graph theory as well as within social systems theory. One may study each single actor, each element, and have a look at his budget: how much value flows into him and how much value goes out? This is an old technique in the analysis of social systems as well, although as mentioned above, we run up against the difficulty of measuring value. But even if this cannot be done with the same (often spurious) exactitudc as in economic analysis it may still be quite indicative in a more crude sense, and help us locate the actors who always profit in their interactive relations, those who always lose, and those who lose in some relations but profit in others so that the net balance is not too bad. Obviously, this can be used to define the upper, lower, and middle classes, respectively, actors in a system.
However, there is another approach that is more fruitful in really using the theory of graphs: focusing less on the individual actor and more on the structure as a whole. And here an impressive amount of parametrization has been contributed by graph theory, particularly by graph theorists who have had some experience with social systems analysis9. An extremely important characteristic of social systems is whether they are strongly, maximally connected (there is interaction both ways in all pairs of actors — often called a primary group); or whether they are minimally connected (there is just enough interaction so that no element is completely isolated — often called a (minimum) secondary group). One might add to this that a “tertiary group”, or just a category of actors, has no interactive relationship at all, such as for instance the class of all long-nosed people.
Once the two extremes of maximum and minimum connectivity have been defined, an index measuring the degree of connectivity can also be introduced, and one can study systems over time. To this can then be added all the measures of distance, some of them applying to individual actors, some of them to the structure as a whole. It should be added that a very important notion on the road from the weakly connected to the strongly connected system is the idea of the cycle, the idea that one can proceed by interactive steps from actor A to B in more than one way. Obviously, this means that the system has several potential channels for the flow of communication, a factor that cannot be overestimated where its social significance is concerned.
Two measures of particular importance in this connection, although they focus our attention for a moment on the individual actors again, should be mentioned. First, there is the idea of associated number: the number of interactive links an actor has. If the interaction is asymmetric one would obviously have to distinguish between interaction from and interaction to, yielding two associated numbers per actor. If the interaction relations in addition are graded, it may or may not (usually not) be meaningful to add the measures for the interactive relations to get a total measure. The difference between the positive and negative measures associated with any one actor would then be the budgetary measure referred to above of net value balance.
The other measure is the measure of centrality. This idea is slightly more complicated. It simply means that one finds the distance, i.e. the minimum number of interactive steps, from each actor to all other actors. This is a set of discrete numbers, and as such it has to have a maximum number10, i.e. the measure of how far away an actor is from the actor farthest away from him in the system, and is referred to as the degree of centrality. Since this measure is unambiguous for each actor, we get one for each of them.
But does this not mean that we have lost sight of the structure as a whole and are now back to a focus on individual actors? No, because we can then start recapturing structural characteristics by studying the set of associated numbers and the set of centrality numbers. In each set we can calculate the average, which is perhaps not so interesting, and the dispersion around the average. Obviously, if the dispersion is zero, if all actors have the same associated numbers and the same centrality numbers, then the structure is egalitarian with regard to these two important characteristics. If it is far from zero it is inegalitarian.
Since structures tend to be inegalitarian in both respects it is important to have some terms for the high and the low on these two important dimensions:
- Actors with maximum associated numbers are high on interactive capacity,
- actors with minimum associated numbers are low on interactive capacity, and
- actors with associated numbers in between are medium on interactive capacity.
- Actors with minimum centrality numbers belong to the center of the structure,
- actors with maximum centrality numbers belong to the periphery of the structure, and
- actors with centrality numbers in between are medium on centrality.
In order to belong to the center of a structure one has to interact in at least two directions; if one interacts in only one direction one cannot help being in the periphery. In general, there is a negative correlation between the associated number and the centrality number, but this negative correlation is not perfect. There is room for variation: the actor with maximum interactive capacity may not occupy the most central position in the structure, and these variations are extremely important in any analysis of social systems.
At this point it should be emphasized that “interactive capacity” does not necessarily refer to the personality or the internal characteristics of the actor. It does not mean that he is more gifted in interaction, more learned, more charismatic or anything else. What it means is simply that interaction in the system is structured in such a way that this is the result.
To what extent the actor can live up to the demand put upon him by the structure is another question. His resources may be on a par with the demands, they may be much above, or much below — and this is again an important perspective in the analysis of social systems.
It should also be noted that the elements in this type of analysis do not necessarily have to be actors; they can also be statuses. This means that the system is no longer what one refers to as an informal system, but a formal system where patterns of interaction have been crystallized and institutionalized to the extent that statuses are defined. Statuses are enacted by means of actors, but have an existence independent of them: they can be seen as holes that have to be filled with actors but that also can be empty (as when an actor disappears from the system for one reason or another and has to be replaced).
In other words, what is characteristic of a system of statuses is replace- ability or substitutability of actors. And this means that all we have said above can be repeated, mutatis mutandis, for sets of statuses instead of sets of actors, and we get an image of formal social systems instead of informal social systems. But from the point of view of abstract analysis there is no difference.
These achievements, and many more along the same line, should not be underestimated. They represent efforts to Capture what is social in a social system; transcending the view of social systems as a heap of detached individuals and the myth that systems can be understood by analyzing the individual actors. The latter view is highly compatible with the type of methodology that converts a set of individual actors participating in a system to a set of IBM cards in order to detect all kinds of properties of the distributions and patterns these actors define on various variables. We do not reject this type of distribution-oriented approach to the understanding of social systems, we only say that it is incomplete, and the parameters mentioned here do the same to structures as the parameters of statistical distribution (and patterns) do to classes of actors. In this there is an important transition from arithmetics to geometry as the language of social research, from parameters that refer to distributions to parameters that refer to structures (and in the latter arithmetics are permitted to reenter the scene again)11.
We will let this do as a presentation of the graph theoretical approach, not because there is not much more to add, but simply because we have not been so impressed with its achievements lately. The insights derived from it have a tendency to become trivial elaborations, often mainly based on combinatorial analyses yielding the number of possibilities of various kinds12. The most important achievement seems still to be the Harary-Cartwright theorem about structural balance, analyzing systems where
there are both positive and negative interacting links. What has happened after that impressive theorem was presented in 1955, stimulating much research and theory formation, seems to have a slightly scholastic tinge. There are of course exceptions to this13, but at this point we prefer to change horse midstream jumping from graph theory to organic chemistry. We shall show that this is a horse that belongs to the same family, yet has some important properties of its own, and very promising prospects.
3. Structuralism and organic chemistry
What we shall have to say in this section about organic chemistry is so ele- mentary and classical that it belongs to old high school curricula. The essential elements in organic chemistry for our purpose seem to be the following: I
- The class of atoms is very small. With C (carbon), O (oxygen), H (hydrogen) one already has the most important building blocks and if to this one adds N, P, S and perhaps Cl and Br and some others, one can account for almost everything. For our purposes, however, we shall restrict ourselves to C, O and H.
- The class of molecules is enormous. These atoms can then combine in many ways to form molecules, and the number of combinations seems to be unlimited.
- The formula of a molecule is determined in three steps:
- The empirical formula, which gives the information about the kinds of atoms that make up the molecule as well as the numerical proportions between them; mC: nO: oH. However, this only determines the formula as (CmOnHo)x where x is unknown.
- The molecular formula. At this stage x is determined, from 1 to any number, and the molecular formula is presented as CpOqHr.
- The structural formula. The important point is now that this formula only determines a class of molecules with the same molecular formula that may nevertheless have very different structures, the class of isomers. When also this formula was determined the work was in a sense terminated in classical organic chemistry, and this is sufficient for our purpose right now.
- Each atom has a valence. The valence is a discrete number which expresses the capacity of the atom to connect to other atoms in a molecule. In our highly conventional organic chemistry these numbers are:
Atom Valence C 4 O 2 H l We disregard atoms with valence zero since “they cannot form molecules (“inactive” gases), we disregard other valences, and we disregard for the moment the important phenomenon that the same atom may under different conditions have different valences. However, we shall not disregard the important circumstance that two atoms may be connected by one valence (single bond) or two valences or three valences (double and triple bonds).
Let us now take an example. We may start with a simple empirical formula of the type (COH2)x where x is to be determined. Analyzing the substance further x is found to be equal to 2 so that the correct formula is C202H4. But this is only the molecular formula defining a class of isomers. Within this class there are two important and different isomers (Figure 6.1).
FIGURE 6.1 Example of isomers, I
H O | // H--C--C | \ H O--H
acetic acid: colorless liquid; strong smell, melting point 16.6°C, boiling point 118.1°C, mixes with alcohol, mixes with water and reacts to some extent forming ions.
H O | // H--C--O-- C | \ H H
methyl formate: colorless liquid melting point -99°C boiling point 31.5°C mixes with alcohol mixes with water
These are not the only theoretical possibilities, however. Figure 6.2 shows two other formulas, satisfying the “rules of the game”.
FIGURE 6.2 Examples of isomers, II
H | O O | // H--C--C | \ H H
glycol aldehyde: colorless crystals, melting point 97° C, mixes with alcohol, mixes with water.
H--O--C==C--O--H
| |
H H
does not “exist”
But let us return to acetic acid and methyl formate. The two compounds have quite different physical properties, and very different effects, when it comes to for instance preparing a salad.
If we now look at these two formulas we see that we are essentially presented with two graphs. However, there is an important difference from what one usually finds in graph theory: instead of a set of indistinguishable elements we now have three classes of elements. Within each class one atom is like the other, but since they may be in different positions they are nevertheless different by virtue of their structural positions. In other words, we have introduced more discrimination, more variety, on the element side. On the relation side, however, some variety is lost: the relationship is symmetric in the sense that there is no distinction between what goes out and what comes in to a position or element. On the other hand, there is a measure of strength in the difference between a single bond and a double bond, but this measure is discrete, it does not admit for more refined nuances. Nevertheless, we shall see that this type of graph makes it possible to discuss problems in social systems that have to some extent escaped attention so far.
If we now look at these two graphs from the point of view of graph theory, we see that they are minimally connected: there are no cycles. Such compounds in organic chemistry are properly known as acyclical, or aliphatic, compounds, and the basic compounds of this kind, with which most textbooks in organic chemistry start, are the alkanes, with the general molecular formula of CnH2n+2, where n varies from 1 (methane) and upwards. In the family of alkanes there are only single bonds, so they are also simple in that sense. But stronger bonds can be introduced, building a progressive series of molecules in Figure 6.3, where progressively stronger bonds are introduced between the two carbon atoms. We have also added one form of carbon (diamond) to show how carbon atoms are arranged in tetrahedrons with single bonds.
FIGURE 6.3 Example of” progressively stronger bonds
C2H6 ethane
H H | | H--C--C--H | | H H
C2H4 ethylene
H H | | C==C | | H H
C2H2 acetylene
H--C≡C--H
carbon
|
C
/ | \
/ _C_ \
C-------C
/ \
Let us introduce some other type of variation. The chemical graphs we have looked at so far are limited in the sense that one could draw a circle around them and say, here it is. However, organic chemistry also has room for endless molecules that just extend and extend, like the important substance in synthetic rubber, isoprene (Figure 6.4) and so on (there may be 4,000–5,000 units of this type chained together). This structure is what accounts for the elasticity of that particular compound.
FIGURE 6.4 Example of non-bounded molecule
H
|
H H-C-H H H
| | | |
. . . - C-----C====C---C-- . . .
| |
H H
It should be noticed in this connection that so far we have assumed that molecules are two-dimensional, that they are planar. However, much more fruitful models from the chemical point of View can be developed if a third dimension is introduced and spatial structural formulas are represented.
But organic chemistry does not stop with the acyclical compounds. It also has cyclical compounds, and here tradition has it that the primordial molecule is benzene (according to one of Kekule’s formulas) (Figure 6.5). (According to more modern chemical thinking benzene is more symmetrical with the six carbon atoms sharing six electrons.) In this particular structure much of the connecting capacity of the carbon atoms is spent on other carbon atoms, in fact as much as 75% (we then count each carbon atom as having four valences, 24 altogether, out of which only six, or 25%, are used to connect hydrogen). If we compare this with, for instance, ethane, the corresponding figure is 25%. Hence, in this particular cyclical structure most of the connective “energy” is between and among carbon atoms; the structure is carbon-oriented.
FIGURE 6.5 Classical benzene presentation
H
|
C
// \
H--C C--H
| ||
H--C C--H
\\ /
C
|
H
And so one could continue, but at this point we feel that there is a need to show where this is leading us. In other words, to what extent, and in what sense, does this give us ideas about social systems?
4. The translation into social systems
What is needed is obviously a dictionary with the terms introduced in the preceding section. One such dictionary is given in Table 6.1.
TABLE 6.1 Dictionary of chemistry — sociology, I
| organic molecules | social systems |
|---|---|
| atom | 1. actor (informal systems) 2. status (formal systems) |
| molecule | system |
| empirical formula | relative numbers of types of actors/statuses |
| molecular formula | absolute numbers of types of actors/statuses |
| structural formula | graph of interaction structure |
| valence | interactive capacity |
| isomers | different structures with the same actors/statuses |
In the following, for the sake of simplicity, we shall use the term actor, which means that we are implicitly talking about informal systems — but what we say is valid mutatis mutandis for formal systems where the elements are statuses.
One basic point is that this model permits us to talk meaningfully about actors of different rank. That is, we have now a way of expressing one characteristic of rank: differential interactive capacity. According to the dictionary this corresponds to valence in organic chemistry, and according to section 2 to associated number (provided the relation depicted is sym- metric and takes into account strength of relations measured in discrete steps).
This can now be expressed by means of a new dictionary (Table 6.2):
TABLE 6.2 Dictionary of chemistry — sociology, II
| Atom | Connective capacity | Actor |
|---|---|---|
| C | 4 | T (topdog) |
| O | 2 | M (middledog) |
| H | 1 | U (underdog) |
Since we have three types of atoms we get three types of actors and we have called them T (topdog), M (middledog) and U (underdog)14. How- ever, it should of course be noted immediately here that there is no reason to stick to the valences that are associated with these particular atoms; any combination of valences or connective capacity, or “interactive capa- city” as it would more properly be called in the science of social systems, can be used.
Each single chemical structure given in the preceding section immediately translates into a social structure. Let us look at some of them, and start with the first two, the isomers acetic acid and methyl formate.
To add some concreteness to it, let us imagine that the topdog is a professor, the middledog an assistant and the underdog a student. The structure of these organizations then looks as follows (Figure 6.6):
FIGURE 6.6 Two isomeric institutes
Institute I
St As
| //
St--Pr--Pr
| \
St As--St
Pr2As2St4
Institute II
St As
| //
St--Pr--As--Pr
| \
St St
Pr2As2St4
In these two institutes not only the proportion between the numbers of professors and assistants and students, but also the absolute numbers are identical. As one sees immediately, the “molecular formula” in chemistry is a “census list” in social systems, it is a catalogue of the types of actors available in the system with frequencies for each. And what is called “struc- tural formula” in organic chemistry becomes “organizational chart” here. The important point is the existence of isomers: with the same composition two institutes may be differently organized. Of course, this is well known —-— it is only that here we have at our disposal a method for systematically exploring the possibility.
In Institute I the two professors interact closely with each other. One of them, the one to the left, may be more teaching oriented and has three students; the one to the right is perhaps more research oriented with his two assistants, one of them a private assistant and the other with some teaching obligations. The institute is professor-oriented.
In /Institute II this has changed: the professors are no longer in direct contact, there is an intermediary, an assistant. The professor to the left is still engaged in his teaching, whereas the professor to the right seems to have divided his obligations. Evidently, the assistant in the middle has a very crucial position, he is the central actor in the system (his centrality number is 2, whereas for both professors it is 3, and for the remaining assis- tant and for all four students it is 4). In Institute I the two professors together share the center since they have the minimum centrality number, 2, whereas the two assistants have the number 3, and all four students are in the periphery, having the number 4. Table 6.3 shows the simple results:
TABLE 6.3 Relations between valence and centrality number
| Valence | Centrality in I | Centrality in II | |
|---|---|---|---|
| Professor | 4 | 2,3 | 3 |
| Assistant | 2 | 4 | 2,4 |
| Student | 1 | 4 | 4 |
It is meaningful to calculate correlation coefficients since these two dimensions are interval scale dimensions, they are based on equidistant numbers that can be interpreted as representing equidistance in systems. The correlation coefficients are -O.82 for Institute I and -0.35 for Institute II, which is a highly synthetic way of expressing how different the two organizations are. Expressed in still different terms: in Institute I there is almost perfect concordance between valence and centrality reinforcing the rank structure; in Institute II this concordance is broken, pushing the professor more towards the periphery and making one of the assistants a highly central person. Everybody who has worked in institutes, or in any other bureaucracy for that matter, knows what a crucial position such an actor may have if he knows how to utilize it, how to convert centrality into power.
Let us now look at some of the other formulas. The formulas for the alkanes are rather boring, but they are more economical in terms of use of professors: the professor-student ratio is n / (2n+2). For n = 1 we have one professor with four students, and so on.
However, what in a sense is highly unrealistic about the use of the alkanes as a model for academic structures is that it presupposes that the links between professors is of the same strength as the link between a professor and a student. For that reason the progressive series ethane-ethylene-etc. is of interest. In ethylene the professors are more tightly connected and this is emphasized further in acetylene. As we progress along this list the professors use more and more of their interactive capacity among themselves, they become more and more research oriented (let us hope) and less and less teaching oriented, until they end up spending all their interactive capacity at the professorial level, for instance in a think tank (pure carbon in Figure 6.3).
But what about isoprene? Does this have any reasonable interpretation? Only in so far as it in a sense is a much more realistic model of social systems that generally interconnect many more actors and statuses than the systems we have discussed so far. Here we have a long chain at our disposal that may, for instance, span around the world as academic interconnections tend to do these days, in postindustrial, neo-modern societies that don’t respect national borders.
Equally interesting is benzene. All we have to do to give an interpretation of this one is to put a circular table in the middle, interpret the topdog as a foreign minister and the underdog as his young assistant, and we get the classical foreign minister conference with the young assistant whispering into the ear of the foreign minister (Figure 6.7).
As we see from the first diagram some foreign ministers are more strongly related than others, and the organizer of the conference has been careful in seeing to it that not all friends are seated on one side; they are interspersed. But it should be emphasized that this latter aspect reflects only the old Kekule formula, not the more modern conceptualization to the right using Robinson’s circle to signify the aromatic sextet of π-electrons (our “table”).
FIGURE 6.7 Two presentations of a benzene-type foreign minister meeting
As
|
FM
// \
As--FM FM--As
| ° ||
As--FM FM--As
\\ /
FM
|
As
As
|
FM
/ \
As--FM FM--As
| ° |
As--FM FM--As
\ /
FM
|
As
We let this do as the illustration, and now turn to some discussion of what has been done so far.
Evidently what we have on our hands is a tool with which we can explore structural variety once the census list of a system is given. Thus, the first problem that immediately presents itself is the question: how many isomers are there, given the composition and the interactive capacity? This problem is being solved by cooperation between chemists and graph theorists, and is now very much a classical problem in organic chemistry15. However, in section 2 we had some rather disparaging comments on combinatorics — and we would immediately say that if this were the only thing we could get out of the type of isomorphism between organic chemistry and social systems we would not think it worth while.
More important is the point that we can put some constraints on our search for isomeric structures. Thus, we might say that we are particularly interested in the structures that have a particularly high or particularly low correlation between valence and centrality; because, for instance, we think they are “good”. Thus, if the correlation is high (in absolute value, that is; generally it is negative) the organization may have a certain stability, although of a highly feudal nature — in fact, this high correlation is one of the characteristics of a feudal system16. If the correlation is low the structure may be less stable; but this instability may be productive. It may lead to more creativity, it may serve to equalize the degree of inequality introduced by the differential distribution of interactive capacity, and thus release resources that are pent up in the more feudal structure.
But this approach presupposes that the distribution of valences is constant. In other words, it does not attack stratification directly but indirectly, although in a very important way, via position in the structure. But just as atoms may operate with different valences in different connections, so may actors and statuses.“ Without necessarily changing them internally we can decide that the distribution of valences shall be different; Table 6.4 shows some ways of doing so.‘
TABLE 6.4 Six distributions of valences
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| T | 4 | 3 | 4 | 2 | 3 | 1 |
| M | 2 | 2 | 3 | 2 | 3 | 1 |
| U | 1 | 1 | 2 | 2 | 3 | 1 |
The first case is the one we have already discussed: there is considerable distance between T and U and in all the other distributions this distance has been reduced. Thus, in the second case the topdog has only three capacities at his disposal (nitrogenl). This reduces the distance from the underdog. but we nevertheless feel that the third case is much more important. Here the difference is also 2, for although the topdog has retained his high interactive capacity, the underdog is now able to relate to more than one. As long as he has only one capacity at his disposal he has to relate to somebody of higher rank (for if he does not, the two underdogs would together spend all their interactive capacity and simply form a pair of friends, U2). When the underdog relates only to somebody of higher rank, the system is at least feudal at the bottom, the underdogs are atomized, disintegrated, as is typical of feudal systems. When he has two capacities at his disposal he can use one for interaction with a middledog or a topdog and one for interaction with another underdog. Thus, in the case of the foreign ministers’ meeting we would get some- thing like Figure 6.8.
FIGURE 6.8 Foreign minister meeting, revised version
As
/ |
/ FM
/ // \
As--FM FM--As
| ° ||
As--FM FM--As
\ \\ /
\ FM
\ |
As
We notice that the formula for this meeting is still FM6As6, as for the former meeting, but since the assistants now are more richly endowed with interactive capacity there are many more possibilities in the system. It should be noted that we have been realistic enough to connect assistants that are the assistants of foreign ministers with particularly strong bonds. However, if we gave to the assistants an interactive capacity of 3, we could connect all of them, so that we would have an inner circle of foreign minis- ters and an outer circle of assistants, and this is of course often a more realistic picture of what happens.
In the fourth case we have equalized the valences completely, which means that we have introduced an egalitarian system. This does of course not mean that the actors or the statuses are completely identical, only that they are identical or equal where rank is concerned. In the fifth case we have given them an additional capacity, and in the sixth case they are also equal but equally poor. This case is only added for systematic reasons: it is a degenerate case since it can never have more than two actors. And if we should be even more systematic we could add the case that all of them have zero interactive capacity, in which case they would be more like hermits in their caves, completely equal in their interactive poverty.
We have just indicated two ways of defeudalizing social systems, and we now turn to some basic questions in this connection. There are some assump- tions underlying all of this. For instance, there is the idea that there are very few basic elements; in our examples we have not exceeded the number 3. However, this assumption is very easily superseded. We can introduce any number of atoms or actors/statuses we want, as long as we have infor- mation about their interactive capacity. Moreover, there is no reason why they should differ in interactive capacity, just as in chemistry they may very well be equal. And just as in chemistry substitution of one actor/ status for another is much more easy when interactive capacity is held con- stant since fewer changes are needed in other places of the system. In fact, organic chemistry can incorporate a high variety of atoms; only that the 3-5 most common atoms combine in such a myriad, such an astronomical variety, of ways that they are more than sufficient.
But we have assumed that actors/statuses, like atoms, are distinguishable. Different atoms have different properties; we assume that this also holds for social systems. This seems to be a reasonable assumption. So much of social life consists exactly in drawing sharp borderlines, particularly between statuses but also between actors. If these statuses are ranked, this is a for— tiori the case, this is the case that interests us most since it is variety in interactive capacity that is the major structural characteristic with which actors and statuses enter these structures. To use the example from academic institutions: the borderline between a student and an assistant is very often drawn using a degree as a criterion, and the borderline between an assistant and a professor is also rather sharp. It may be objected that this is not so much the case between actors, they more fade over into each other. However, this only means that we can group together actors that belong to the same equivalence class and give them the same symbol, and give another symbol to actors that are clearly distinguishable from the former.
What about the corresponding assumption of interactive capacity as a discrete variable? Again it seems that the isomorphism is rather good. The interactive capacity of carbon is set like 4, not like 3.9 or 4.1, since it connects with discrete entities according to this model, with other atoms (some of which may be other carbon atoms). Similarly, an actor interacts with discrete numbers of actors, not with 3.9 or 4.1 actors (some of them may be of the same kind as himself), and the same applies to statuses.
Where the isomorphism breaks down is the discreteness where strength of the bond is concerned: here it is obvious that the social systems offer much more variety than this model of chemical systems seems to offer. But as long as there is some proviso for this idea in the idea of the multiple bond, we are not too worried. Moreover, in modern chemistry graded bonds or “bond-orders” have been introduced and they take on the values 1 when there is a single bond (like in ethane), 2 when there is a double bond (like in ethylene) and 3 when there is a triple bond (like in acethylene). Thus, in butadiene the formula is:
FIGURE 6.9 Example of graded bonds
H2C ==== CH ---- CH ==== CH2
1.89 1.45 1.89
In other words, modern chemical thinking seems to come much closer to social science thinking than does more classical thinking.
There is also another parallel which we have not explored but will just mention: the idea of free valences, of connective or interactive capacity that is unused. Atoms in ionized form are clear examples and may also be found inside molecules. Similarly, an organization of a social system may not utilize all interactive capacity; there may be free capacities available, and these capacities may for instance be used to connect with free capacities in other systems, forming a supersystem.
However, there are at least three points at which the isomorphism devel- oped so far breaks down.
First of all, as already pointed out: the interaction relations taken care of by this model are all symmetric. This highly important aspect of class, the exploitative aspect leading to positive accumulation on the top and negative accumulation at the bottom, does not enter here at all. In order to make it enter, we might have to operate with two kinds of valences: valences in and valences out, interpreted as interactive needs and interactivc capacities, respectively. But there is also another approach: in modern chemistry there seems to be more room for the idea that one atom is “exploit- ing” another by; appropriating to it much more of the electrons in a bond than the neighbor does17.
Secondly, this model does not take into/account negative interaction. The valences connect, they attract; they do not reject, repel and hence disconnect. In social systems this is as important a reality as the positive ties, and a particularly important focus of analysis of social systems is how it is possible to contain forces of rejection within a system. Thus, one could imagine negative valences being contained at or close to the center of the system because it is surrounded by so many positive valences18.
Thirdly, there is the important transition from social system to social structure. An actor participates not only in one system but at the same time also in other systems. Some of the systems may be informal, some formal, but he occupies positions in them all. The systems may be isomorphic and all actors may connect corresponding positions, in which case he would obviously have to have the same interactive capacity in all of them. But they may also be non-isomorphic and the actor may occupy non-corresponding positions, so that even if he is high on valence in one system he may be low on another. All combinations are possible here, in principle, although there may be a tendency towards feudal structures which are based on congruence, on replication. Such a set of systems interconnected by the circumstance that the same actors appear in all of them is called a social structure.
According to our dictionary it would correspond to a set of molecules, and the idea of bonds between the molecules is by no means unknown to chemistry19. But there is an important difference here: in chemistry the model is usually that the forces within the atom are much stronger than the forces between the atoms in a molecule, and these forces in turn are much stronger than the forces between molecules. In social systems the former relation often holds; cohesive forces within actors are stronger than cohesive forces between actors, but the latter cannot be said to be stronger than the forces connecting systems since these forces are the actors themselves. If I am both a director of an institute and a professor at a university, I serve to connect the two systems and this force in me may be stronger than the force connecting me to role partners in both systems.
We would also like to emphasize one shortcoming that graph theory and chemical graphs have in common: as they are generally presented with these classical structural formulae the relations are bilateral. In social systems, however, multilateral relations are just as, or even more, important, and although there are very significant parallels to this in chemistry (as seen when one proceeds from planar to spatial structural formulae), they are not captured by the simplistic formula we have so far presented20.
However, these are problems that can be explored later. Nothing but the social system itself will ever be a perfect model of the social system; we cannot expect in general to capture much more than we have already caught in this isomorphism net. Classical chemistry used to distinguish between 92 different kinds of atoms, today the transuraniums have been added, bringing the number up to above 10021. This is obviously much less than the number of occupations listed in the census lists of “modern” countries, particularly countries with rich, differentiated tertiary sectors. On the other hand, what is so impressive about chemistry in general, and organic chemistry in particular, is the very high number of combinations that are made using a very small number of building bricks. In social systems in general and societies in particular it looks as if we have many more building bricks but much less variety in the combinations. And one reason why this seems to be so will be explored in the next section.
5. The transition from analytical to synthetic chemistry
From our point of View chemistry represents an extremely challenging case in the history of science, with two phases that we shall, in a highly simplified manner, describe as the phases of analytical and synthetic chemistry.
In the first phase, analytical chemistry, there was the general image that Nature was rich, abundantly rich, in variety. Once laboratory techniques were developed there was the fascination of dissecting all the physical mixtures presented by Nature into their chemical compounds in order to proceed with the pure compounds (those that had invariant physical properties) so as to determine first the empirical formula (according to the laws of constant proportions), then the molecular formula, and finally the structural formula. It is indeed impressive what was done in those years in gaining understanding of chemistry. Nature was analyzed, the empirically given was seen under unifying perspectives, order was brought into a seemingly chaotic system.
And yet, it is the second phase, synthetic chemistry, that in our mind makes chemistry great, perhaps from this perspective the greatest of all sciences, with organic chemistry as the queen. The idea was gotten that once the building bricks were given, they could perhaps also be combined in ways that have so far not been represented in Nature. And once this mental jump was made, an extremely audacious one, the laboratory search for “artificial” compounds started and soon produced new actual and also potential variety much beyond what Nature had ever dreamt of. Nature was seen as a special case of what is potentially possible. There was of course some kind of explanation for this: since Nature has only lasted for so and so many years, and since some time is needed to bring about all the possible permutations of atoms in a sufficient proximity and under conditions that make them combine into new molecules, it may very well be that, given some more billion years, Nature might produce much more than the laboratory has ever dreamt of. But this was not necessarily the case, and the distinction between natural and artificial compounds was thus established.
This was not an easy step to take, as is well known in connection with the Wöhler synthesis in 1828. The argument was: if these synthetic compounds (although Wöhler did not synthesize an unknown compound but a known organic one) had been intended by God to exist, then Nature would already have had them. In other words, the model of nature before the second phase in chemistry presented the characteristic discontinuity between what is actually realized and what is conceivable (Fig 6.10).
FIGURE 6.10 The empirical and the conceivable — two models
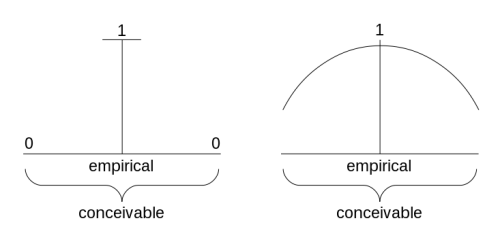
What is conceivable but not empirical was somehow given the weight of zero; what was empirical was given the weight of 1. Of course, this conception was highly compatible with the idea of a nature created by God: man may conceive of other worlds, with other compounds, but God did not create them because he did not want/saw no need for them to exist. God initiated, and terminated, creation.
With the entry of synthetic chemistry on the scene this distribution looks different: there was of course still the distinction between the empirically given, the “natural”, and the conceivable, and the word “synthetic” still has a connotation of “artificial” (although many synthetic materials are superior from many points” of view to what Nature has produced, for the simple reason that they are made to order). The distinction between the . empirically given and the synthetically created is blurred, and increasingly so.
However, there is still the idea that something that is conceivable is less possible: there is the idea of unstable elements (an unfavorable balance between neutrons and protons) and unstable compounds. In other words, a new distinction is introduced: between the compounds that Nature has not produced (so far) and that can exist in nature under normal conditions, and the compounds that require special conditions. They require special conditions not only to be brought into being, (such as combinations of pressure and temperature far away from the standard conditions of 760 mm and 0° Celsius or 15° Celsius, or the presence of catalysts, bombardment with radioactive particles and so on); they also require special conditions to survive for any length of time. “Normal conditions” are anthropocentric conditions under which man normally lives — they should not govern our thinking about Nature too much, however.
And this, then, leads to the next question. From asking: “What is so holy about what Nature has produced relative to what it has not produced?”, one may proceed to the question: “What is so holy about the external conditions present in our daily life?” Just as the answer was “nothing” to the first question, it may also be “nothing” to the second. But the two questions are of course related: under the external conditions in which we pass our physical existence, with the limited variations available on the surface of the earth, some compounds that are conceivable are more likely than others.
But the basic point here is that we are now led to formulate the whole question about the relation between Man and Nature in a completely different way. Instead of asking what Nature is most likely to realize under the present conditions, we may ask under what conditions we together with Nature may realize what we want22. If we want some particular chemical com- pound for some purpose, than let us create the conditions under which it can exist. To take a parallel from physics: if we want conductors with as close to zero resistance as possible, then let us make use of kryogenics; let us create the conditions close to absolute zero where these conductors ‘ exist, and make use of them. The fact that we may not ourselves have a present existence under that circumstance is immaterial; we have means of isolating ourselves from the conditions.
Epistemologically speaking the distinction between analytical and synthetic chemistry is the distinction between what in Chapter 2 we call, respectively, empiricism and constructivism. Under strict empiricism one accepts model 1 above: Nature is given and what is conceivable but not empirical is uninteresting. Under this slogan empirical social science consists in analysis of existing systems, of human relations area files of correlating whatever exists in all directions until everything is dissected. Under constructivism, which corresponds more to model 2, one would use these elements of analysis and try to combine them in new ways. Instead of merely proceeding analytically with social systems, one would proceed synthetically, combining the combinable in new ways, guided by theory and values.
This is of course by no means new to humanity. Utopians, ideologists, politicians are doing this all the time, in their books, manifestos and programs — and they may translate it into political reality. The difference between this and chemistry is only that in chemistry empiricism and constructivism coexist within the same mind: it is the same chemist who does analytical and synthetic work (or even if there is a division of labor, there is excellent communication). The moment the social scientist subscribes to empiricism and closes himself off from constructivism, he produces so-called value-free science, which is only in this case another way of saying that he acts as if what so far is empirically given is the only thing that can be empirically given. In other words, he is in a peculiar sense on the side of those who resisted most energetically the emergence of the synthetic phase in chemistry.
Hence, this turns into an argument in favor of combining empiricism with constructivism, not an argument in favor of rejecting either of them. And again, just as in chemistry, the creation of a new social system may not take place under normal conditions. The changes may take place, for instance, under the conditions referred to as revolutions (high pressure, high temperature?), under the conditions referred to as presence of an innovator (the presence of a catalyst?), or the conditions referred to as bombardment; in this last case not of particles of energy stemming from radioactivity or cosmic rays, etc., but the type of bombardment known as a war. It may also well be that they can only be maintained under “artificial” conditions, such as a crisis, an extreme challenge from the outside (for instance as produced by economic sanctions). The isomorphism is also here of a rather impressive nature, except for the point underlined above: there is a division of labor when it comes to empiricism versus constructivism in social systems that is not found in chemistry.
It is hardly necessary to add that there is no implicit assumption here hat there also should be a transfer to social systems of the relationship chemists have to their compounds. We are not in any sense arguing that the social scientists should become social engineers like the chemical scientist is a chemical engineer, manufacturing new compounds to order, given certain goals presented to him by clients, employers, etc. We would see this as a common concern involving all participants in the system equally, as a creative mobilization “under a banner of constructivism, and we feel that it could be guided better by more insight into what empirical social science has to give and what the values mean translated into terms that are meaningful in understanding social systems.
And this leads to our final point. It is so often said that sociology is underdeveloped, and those who say so usually compare it with physics and point out that sociology cannot measure, cannot develop, invariances with a high level of specificity, cannot develop theories with a high level of deductivity, and so on. We have in Chapter 2 criticized these assumptions, at least to our own satisfaction. But that does not mean that we do not agree that sociology is underdeveloped, only that we would use a different criterion.
We would say that sociology is underdeveloped because there is so little focus in sociology today on the good social system, on the good society. Under criticism and “value-free” empiricism such speculations have been banned. Social scientists have not done what chemists are doing, defining the “good chemical compound”, which is the compound that has such and such specified characteristics. They have not done what the physical scientists do when they develop the good alloy that can serve the purposes needed for instance in a space ship. These people are not limited to what is given by Nature, but combine known elements in completely new ways. Social scientists are more like the biologists who up till now have shown respect for the empirically given, and only recently have started speculating how human beings can be improved upon, instead of accepting it as an eternal invariant. That this also opens the possibility of doing worse than Nature goes without saying — leading to the empiricism of “we know what we have but not what we may get”.
6. The transition from classical to modern chemistry
There are interesting parallels not only between social and (organic) chemical structures, but also in the way thinking about them is changing. Since there is little or no intellectual contact between these two fields the parallel must either have come about by chance, which is not very likely, or be due to deeper phenomena, even to common factors.
One such common factor is simply the transition towards more complex forms of understanding. Starting with bilateral interaction between human actors and the Lewis model in chemistry the next steps will almost have to be in the direction of grading the strength of the bond, of making the relation less symmetric, of providing for negative relations of repulsion, of bringing in multilateral relations in addition to bilateral and the Chinese boxes ideas: subunits are tied together in units, these are tied together in superunits, etc. The intellectual history of organic chemistry and structurally oriented social science is probably relatively similar here: there is the bewildering complexity both of the individual society/compound and of the variety of societies/compounds; there is the effort to come down to the basic unit, which is not the individual/atom but individuals/atoms and bonds. A concept of connecting capacity enters the picture, and there is the idea of limited connecting capacity, at least of the direct and strong variety23.
Then there is the process of building upwards from this base, in the ways indicated, to try to recapture the structural complexity that was the point of departure. Chemistry has precise measurement and experimentation much more at its disposal than the social sciences do; but the structures are nevertheless similar and social science has the empathy of the individuals to draw upon for inspiration and for criticism. As to the latter: if atoms could speak, they might have a couple of things to tell the specialists; not necessarily that they are wrong, but that they are exploring unimportant, irrelevant dimensions.
But then there may be another factor steering the intellectual development in the same direction; a general shift in emphasis towards the more discontinuous, the more extreme, rather than just studying the smooth and the normal. In chemistry, quantum mechanics was a mental breakthrough, just as dialectic thinking, especially through marxism, was for social science: it paved the way for “jumps”, discontinuities. Correspondingly the study of high/low temperature etc. chemistry has its parallel in the study of society under extreme conditions, e.g. concentration camps, or total institutions (prisons, mental hospitals, etc.) The normal was to be understood as special cases of a much broader range of presentations of Nature/Society, and in order to prepare the ground for this the basic units had to be made sufficiently complex. There was the need to go deeper into the basic units, getting at basic components, and this dissection of the individuals was done by psychoanalysis (and related approaches) in social science and, for instance, by nuclear chemistry and physics; the insights gained were tied to the theory of interaction/bonds, which then appeared much more fragile and complex than they had before, but also more capable of variety and for that reason more realistic. At this point there is a division between the two: where social science tends to explain micro-configurations by means of macro-configurations, chemistry tends to do the opposite. An educated guess might be that they will converge in the future: that social science will see society more as created by individuals (e.g. by giving individuals a deeper structure) and chemistry will see the micro level more as constituted by the macro level. In either case the old controversy between particle perspective and some kind of field perspective is discernible.
However this may be, another educated guess would be that chemistry, like nuclear physics, is in a phase of accumulation of insights, data, models that will lead to a qualitative jump synthesizing much that today may look contradictory, generating a higher and possibly simpler approach. No doubt that approach may have important messages for social science.
More particularly, there is one field in which much progress could be made: transformation theory. In organic chemistry excellent tools exist for presentation of the structure of molecules, but perhaps not for the process for transformation from one set of structures to others. In social science analysis an interaction matrix is one such tool. Given two such matrices, M1 and M2 for the same In actors at two points in time or space (they may change pattern over time or have a different interaction pattern in some other interaction context), a transformation matrix T so that M2 = = TM1 is easily found. What is not easily done, however, is to find a form of presentation so that the transformation factor or function can be identified, component for component, with concrete components in the transformation process itself. In classical chemistry the model was budgetary: one compound “plus” another compound “equal to” or “leading to” a third compound (plus/minus energy in some form). But this was an unfortunate form of presentation for it does not present the details of the trans- formation process, only catalogues“ of inputs and outputs and even that in a sometimes misleading manner (thus, the associative law is not valid and sometimes neither is the commutative law — both of them suggested by the arithmetic symbolism). The symbolism also tends to tie the models to classical “change in variable X leads to change in variable Y” (keeping all other variables constant, usually by disregarding them) thinking, rather than to more holistic approaches dealing with a total configuration of variables — in other words, transformation of structures24.
We let this do as an illustration of possibilities for the future in pursuing further this interesting parallel in intellectual development — no doubt of interest to social scientists, one day possibly also of some interest to physical scientists.
7. Conclusion
The goal of this very simple exploration has been not to lose contact with the socially relevant. One socially relevant factor is what might be called structural imagination, where a look at a textbook of organic chemistry and a textbook of, say, sociology, gives a clear indication of where this factor is more developed. Social scientists talk about human and social variety, the specialists in organic chemistry not only talk about it, but present it and produce it. In this there is much to learn, but there is also much to learn from the way chemistry has managed to integrate empirical and constructive approaches. The critical approach, however, is considerably less developed: “critical chemistry” as socially conscious chemistry, seems more to be something imposed upon the discipline from the outside than something builti nto the discipline itself although this may be changing.
But could we not have arrived at all of this while staying within graph theory? In fact, is it not all to some extent incorporated in graph theory as witnessed by the circumstance that graph theory has been an important tool in theoretical chemistry? There is something to this, but there are also important differences between fetching models from mathematics and from another substantive discipline. Firstly, as we have pointed out, there may be some underlying similarity in the way the two subject matters are viewed, leading to parallel developments. Secondly, it takes time before insights into a substantive discipline find or stimulate a counterpart in a formal discipline like mathematics. And finally, there is a similarity between researchers in the two fields, who are trying to come to grips with complexity, oscillating between the empirical and the potential — possibly steered by some principles governing the relation between the two, but so far’ hidden to us — which leads to reservoirs of similarity in basic concepts and insights.
Notes:
- I am indebted to seminar participants, particularly M. Malitza, S. Marcus and A. T. Balaban; and also to A. Hartmann, J. W. Ulrich and T. Judge. They should not be held responsible for any errors in this expression of my lasting romance with chemistry, however, starting when I was 12 years old.
- Thus, structuralism is more pure than functionalism, based merely on the idea of elements and relations; there is no directedness built into it at this minimum level.↩
- Marxism would be a good example here with its emphasis on the tight coupling between structural elements in the infra- and super-structures, as pointed out in the preceding chapter. But Marxism also has a pronounced element of directedness, only that it is not inside the same structure but based on a very comprehensive transcendence. Thus, where conservative functionalism has directedness in the sense of regeneration, liberal functionalism in the sense of evolutionism, reformism along one or a couple of dimensions, radical functionalism and Marxism operate in terms of transcendence. The difference between them would be that radical functionalism emphasizes much more the volitional aspect, the choice of values (function) and the search for new structure (s) that would make for a well integrated s, f-matrix; Marxism centers more on the unavoidability — at least in the longer run — of the transcendent processes. It is more purely structural, but also, deed, process-oriented.↩
- Another example, more politically meaningful, would have to do with the relations between the big powers:
Occidental Oriental Capitalist US (EC) Japan Socialist SU China They constitute a structure not only in the sense that there are relations between them, but also in the sense that there are relations between relations. Thus, it may be argued that “Japan relates to China as the us relates to the Soviet Union”; cold war tension in one pair, or passive co-existence, or active co- existence are accompanied by the same relations in the other pair. Something of the same might be postulated for us: Japan relative to Soviet Union: China, only that the cultural revolution liberating Japan from the US so far fizzled out (both the Japanese student revolt, and the Mishima suicide can be seen as attempts in that direction). And the third relation is also interesting: when US opened up for relations with China, Japan had to do something of the same relative to the Soviet Union — only that in this case it may be argued that Japan was first.
For more details, see “Japan and Future World Politics”, Essays, V. 6. The point here is that bilateral relations between two attributes of the units (the big powers) would be incapable of handling the nature of this relation.↩
- That it is intuitive is no objection, but there is a vagueness about basic concepts. See the critique by Francis Korn, An Analysis of the Use of the Term “Model” in Some of Levi-Strauss’ works, Bijdragen, Deel 125, 1969, pp. 1-11.↩
- See the fascinating essay by Andre Weil, “On the Algebraic Study of Certain Types of Marriage Laws (Murngin System)”, Appendix to part one of The Elementary ‘Structures of Kinship by Claude Levi-Strauss (London: Eyre & Spottiswood, l969) — translated from the original Les Structures Elementaires de la Parente, from 1949. I am indebted to Sverre Holm who drew my attention to this work when I was a student of mathematics and sociology in 1952. A fine introduction to Lévi-Strauss is given by Edmund Leach in the Fontana Modern Masters series (London: Collins, 1970).↩
- For an introduction to Chomsky, see John Lyon’s book in the Fontana Modern Masters series (London: Collins, 1970). Or Chomsky’s own books. Language and Mind (New York: Harcourt, Brace & World, 1968) is an easy introduction.↩
- What is more dignified, to be firm and rigid, or — more malleable and flexible? No doubt behaviorist man was malleable and manipulable, but what about this new man with so many structures engraved on his mind — is he not too predetermined? Or maybe a better approach would be to focus attention more on the structure of society than on the structure of the mind and think in terms of internalization of the social grammars in a mind that somehow is prepared to receive them. This approach is basic to the work on social cosmology within the “Trends, in Western Civilization Program”.↩
- There is a principle here: mathematics should not be too much removed from other ways of exploring social affairs; our experience seems to be that when it is, the results are not very interesting because they are so removed from social reality as commonly conceived of. The approach would only cater to elite interests in having their own keys to social reality, inaccessible to anybody else.↩
- Cartwright and Harary are, of course, the important names here. See F. Harary, R. Z. Norman, D. Cartwright, (eds.) Structural Models. An Introduction to the Theory of Directed Graphs (New York: Wiley, 1965).↩
- If the graph is finite as we assume it to be since it mirrors a finite system, human societies.↩
- This is a major aspect of the “World Indicators Program“ at the Chair in Conflict and Peace Research, University of Oslo and Institut d‘Etudes du Developement, Genéve: indicators are interpreted not only as numbers, but also as graphs.↩
- The reason for this is possibly that there is still the assumption that real information is numerical information, in other words that parametrization of graphs — distances, associated numbers etc. — is the ultimate goal. Somehow we are not sufficiently trained in appreciating graphs just as graphs, as structure per se. The same problem is found in indicator-formation where it is taken for granted that an indicator has to be numerical, not just structural.↩
- An interesting approach is made by Nils Petter Gleditsch and Tord Haivik, “Structural Parameters of Graphs”, originally published in Quality and Quantity. Later in Blalock et al., Quantitative Sociology (New York, Academic Press, 1975) pp. 203-223.↩
- For some explorations of this theme see the first six essays in Essays, vol. III — particularly “Rank and Social Integration: A Multidimensional Approach (III. 5).↩
- See, for instance, the very impressive series of articles “Chemical Graphs” by A. T. Balaban of the Institute of Atomic Physics in Bucharest ( e.g. no. IV with F. Harary in Revue Roumaine de Chimie, 1967, pp. 1511–15; no. V with F. Harary in Tetrahedron, 1968, pp. 1505–16; no. V1 with C. C. Rentia and E. Ciupitu in Revue Roumaine de Chimie, 1968, pp. 231–47; no. VII in Tetrahedron, 1969, pp. 2949–56, no. IX with D. Farcasiu and F. Harary in Journal of Labelled Compounds, 1970, pp. 211–223, no. XIX in Revue Roumaine de Chimie, 1973, pp. 635–53 — and “Cubic Identity Graphs and Planar Graphs Derived From Trees”, with R. 0. Davies, Frank Harary, A. Hill and R. Westwick in The Journal of the Australian Mathematical Society, 1970, pp 207–15). No doubt this tradition will sooner or later lead to new breakthroughs, perhaps also with major simplifications.↩
- For a presentation of this approach, see “Feudal Systems, Structural Violence and the Structural Theory of Revolutions”, Essays, III. 7.↩
- The asymmetry comes into the picture in connection with the type of covalent bonds where electrons are “donated” from one atom and “accepted” by another. One could imagine a continuum here, from perfect sharing of electrons to “appropriation” by some atoms, or group of atoms, more than others. In general, if some atoms are very electro-positive and others slightly electro-negative, the interaction between them is not symmetric whatever the valences.↩
- One example here would simply be an ion. But in general there can be forces of repulsion between atoms in molecules and between molecules in super-molecules, but more than counteracted by forces of attraction. The shape of the molecule or super-molecule will then be determined by the balance of these forces, as equilibrium positions, and, of course, in three-dimensional, not only the two-dimensional space of the classical model. In human relations all one has to do is to watch seating patterns at a faculty meeting to see how people arrange themselves so as to be with friends and away from enemies. But free valences can also be illustrated by “a large crowd of foreign male workers in some European countries, or lonesome teenage males on the hunt for a girl in a nightclub district” (suggested by Tony Judge). Thus, a free valence can be seen as a free linkage capacity, not as a force of attraction or repulsion.↩
- The inter-molecular bonds do this for chemistry. Molecules are not perfectly balanced, neutral, as they appear according to the classical Lewis models from 1916, based on the octet rule around which most of the present paper is built. Molecules may be polarized when based on covalent bonds and behave like small dipoles with the negative pole from one molecule coming close to the positive pole from another and poles with the same sign rejecting each other into equilibrium positions. Then, dipoles may attract ions as when water, which is polarized, easily dissolves (“attracts”) compounds with ion bonds. Then there is the hydrogen bond between a hydrogen atom linked to a very electro-negative atom in one molecule and a very electro-negative atom in another molecule. Thus, hydrogen atoms — the extreme periphery of the molecule in organic chemistry according to the Lewis models — appear as connecting links between molecules, like children may connect families. Finally there are the dispersion bonds, based on self-polarization of unpolarized molecules. See P. Gaede and J. Ulrich, Strukturer 0g Mekanismer i Organisk Kemi, Copenhagen, Ejlers, 1973, pp. 59–61. Under such perspectives the “inactive” gases also become less inactive (van der Waal forces).↩
- The π-bond, as opposed to the σ-bond, can be seen as such as “multilateral” bond where more than two atoms share electrons (an indication is given in Figure 6.7), the G-bond being bilateral. Just as for social structures “the π-bond is broken relatively easily, giving rise to two σ-bonds in the process” (from Werner Herz, The Shape of Carbon Compounds, New York, Benjamin, 1964, p. 34 — discussing alkanes). Also see the classic, Linus Pauling, The Chemical Bond (Ithaca: Cornell University Press, 1967); particularly Chapter 1.↩
- One hundred and four if we count to 104 Ku. The trans-urans, and also some of the cis-urans, break down because they are oversized. A parallel to oversized superstates…? Or to overloaded individuals?↩
- This was the problem with which the Theory and Methods of Social Research was concluded (p. 488 in the same collection): instead of asking, “given a set of specified initial conditions c, what is the most likely state of the world s that will follow from c” one can also ask the question “given a state s* of the world, which are the conditions c* that are most likely to produce s*“. “The former limits the range of variation in human affairs, the second leaves it open — even enlarges the range”.↩
- There is a long tradition in the social sciences, e.g. associated with J. Miller. to the effect that there is a limit to the discriminatory power of human beings, Curiously enough the number 7 also figures here—when the number of elements to relate to becomes (much) higher they are handled conceptually by lumping them together in classes. When the “elements” are other human beings this means stereotypization, bureaucratization.↩
- However, as usual chemistry is far ahead, the presentation forms are rapidly changing, bringing in Gibbs energy and sequences of elementary mechanisms. Still, there is work to be done.↩
This is an author copy republished by TRANSCEND Media Service in April 2018. This article was first presented in May 1974 at The International Seminar on Mathematical Approaches to International Relations, Poiana Brasov, Rumania. It was later published as chapter 6 in Peace and Social Structure. Essays in Peace Research Volume III (1978), pp. 160-189.
Prepared by Naakow Grant-Hayford and Malvin Gattinger
 Johan Galtung, a professor of peace studies, dr hc mult, is founder of TRANSCEND International and rector of TRANSCEND Peace University. Prof. Galtung has published more than 1500 articles and book chapters, over 500 Editorials for TRANSCEND Media Service, and more than 170 books on peace and related issues, of which more than 40 have been translated to other languages, including 50 Years-100 Peace and Conflict Perspectives published by TRANSCEND University Press. More information about Prof. Galtung and all of his publications can be found at transcend.org/galtung.
Johan Galtung, a professor of peace studies, dr hc mult, is founder of TRANSCEND International and rector of TRANSCEND Peace University. Prof. Galtung has published more than 1500 articles and book chapters, over 500 Editorials for TRANSCEND Media Service, and more than 170 books on peace and related issues, of which more than 40 have been translated to other languages, including 50 Years-100 Peace and Conflict Perspectives published by TRANSCEND University Press. More information about Prof. Galtung and all of his publications can be found at transcend.org/galtung.
Tags: Research, Sociology
This article originally appeared on Transcend Media Service (TMS) on 23 Apr 2018.
Anticopyright: Editorials and articles originated on TMS may be freely reprinted, disseminated, translated and used as background material, provided an acknowledgement and link to the source, TMS: Structural Analysis and Chemical Models, is included. Thank you.
If you enjoyed this article, please donate to TMS to join the growing list of TMS Supporters.

This work is licensed under a CC BY-NC 4.0 License.
Read more
Click here to go to the current weekly digest or pick another article:
FEATURED RESEARCH PAPER: